黄焖鸡起源于济南名店“吉玲园”,属于中华传统炖煮类肉制品,主要食材是鸡腿肉,配以青红椒等辅料焖制而成,味道鲜美,深受广大消费者的喜爱。为了最大程度地保留黄焖鸡的营养成分和风味特性,低温杀菌是实现上述目的的重要方法,但也造成了原料肉及加工过程中污染的微生物难以被彻底杀灭,在一定贮藏条件下,产品中残存的微生物容易大量生长繁殖,导致产品的食用品质出现劣变,甚至对消费者的健康产生危害[1]。因此,对低温杀菌黄焖鸡产品在常见贮运温度下微生物的生长情况进行监控,对同类型产品的品质控制具有非常重要的现实意义。
预测食品微生物学(predictive food microbiology,PFM)是以计算机技术为基础,综合数学、微生物等相关知识,对食品中微生物的残存、生长、延迟和死亡等过程进行数量化预测的一门综合性技术[2-3]。微生物生长预测模型是以预测食品微生物学为基础建立的预测工具,分为一级模型、二级模型和三级模型,其中一级模型和二级模型为微生物生长动力学模型,三级模型是将一级模型和二级模型通过计算机软件形式合并得到的模型形式[4-5]。根据微生物生长预测模型推算出的相关参数可以建立食品的货架期预测模型,实现对食品安全性和剩余货架期的快速预测。
近年来,已有许多学者对肉及肉制品中微生物生长预测模型的拟合优度(goodness-of-fit)进行了评价,其中回归相关系数R2、均方误差平方根(root mean square error,RMSE)、赤池信息准则(Akaike information criterion,AIC)与贝叶斯信息准则(Bayesian information criterion,BIC)是最常选用的模型评价指标[5]。通过模型评价指标的比较,能够反映各模型拟合效果的优劣,有助于选择适合产品的微生物生长预测模型。朱彦祺等[6]通过比较R2、RMSE、AIC及BIC等模型评价指标,确定修正的Logistic模型的拟合优度高于修正的Gompertz模型和Baranyi模型,该模型能够很好地描述水产品中腐败希瓦氏菌的生长情况;Yang等[7]分析残差平方和(residual sum of squares,RSS)、皮尔逊相关系数(Pearson correlation coefficient)、AIC及BIC等指标的差异,确定出Arrhenius模型的拟合效果最佳。但是,目前国内外的相关研究主要集中于冷鲜肉,与肉制品相关的研究较少,对低温杀菌黄焖鸡中微生物生长预测模型的比较研究未见报道。
本研究探讨低温杀菌黄焖鸡于4、15、25 ℃条件下贮藏时菌落总数的变化情况,利用修正的Gompertz模型、修正的Logistic模型和Baranyi模型拟合菌落总数的生长情况,利用Belehradck模型和Arrhenius模型研究菌落总数生长参数与温度之间的关系,通过计算模型评价指标比较各模型的拟合效果,选择最优的模型组合进行产品的货架期预测,为该类产品的安全流通和销售提供理论参考。
50 只新鲜黄羽肉鸡琵琶腿。黄羽肉鸡来自于集中饲养,屠宰平均日龄49 d,体质量(2.00±0.23) kg。低温杀菌黄焖鸡加工过程中所用的材料均为食品级。
氯化钠(分析纯) 北京索莱宝科技有限公司;平板计数琼脂、无菌拍打袋 北京陆桥技术有限责任公司。
PB2002-N电子天平 梅特勒-托利多仪器(上海)有限公司;DF-6L专用油炸锅(额定功率2.3 kW) 广州杰冠西厨设备厂;BCD-251 WBCY冰箱 青岛海尔股份有限公司;HHS11-1电热恒温水浴锅、LRH-250F生化培养箱、YXQ-LS-100A立式压力蒸汽灭菌器(额定功率3.6 kW) 上海博讯实业有限公司;SW-CJ-2D超净工作台 济南道迪医疗器械有限公司;Research plus单道移液器 艾本德中国有限公司;JT-10拍打器(3~12 次/s) 杭州聚同电子有限公司。
1.3.1 样品制备
参照常思盎等[8]的方法,并略作修改。称取约10.00 kg带骨琵琶腿段切成3 cm×4 cm大小的肉块,添加2.00%的食盐、0.20%的白酒(酒精度38%)和0.20%的姜黄粉(所有比例均为材料质量占鸡肉质量的百分比,下同),于4 ℃条件下腌制30 min;按照油料比4∶1(m/m)向油炸锅内加入新鲜橄榄油,将腌好的鸡肉块下锅,180 ℃油炸30 s,沥油备用;向炒锅内加入3.00%的新鲜橄榄油,加热至微沸,加入0.50%的姜片和青红椒段炒香;向锅内加入50.00%的水,依次加入0.35%的白糖、2.00%的黄豆酱、1.50%的鲜鸡汁和炸鸡肉块,锅内温度100 ℃焖制10 min。
将制备完成后的黄焖鸡进行分离并冷却至常温,采用真空包装,每袋质量(120.00±10.00) g,共135 袋。包装完成后,立即对样品进行巴氏杀菌,杀菌温度85 ℃,杀菌时间15 min。
1.3.2 实验设计
将制得的135 袋样品随机等分成3 组,并将分组后的样品置于4、15、25 ℃条件下贮藏,定期从每组样品中分别取出3 袋进行菌落总数测定,取3 次测定数据的平均值进行后续建模。样品在4、15、25 ℃条件下的取样间隔依次为14、7、2 d。
1.3.3 菌落总数的测定
无菌条件下准确称取4、15、25 ℃条件下贮藏的黄焖鸡样品25 g,用无菌剪刀剪碎,加入盛有225 mL灭菌生理盐水的均质袋中,封口后用拍打器拍打2 min,制成1∶10的样品匀液。选择3 个合适的稀释梯度,每个梯度做3 个重复,倾注平皿(平板计数琼脂)。将平皿于37 ℃培养箱倒置培养48 h,按照GB 4789.2—2016《食品安全国家标准 食品微生物学检验 菌落总数测定》[9]的方法进行计数。
利用SPSS Statistics 20软件(美国IBM公司)中的单因素方差分析进行数据分析,显著性水平P<0.05;利用Origin 9.0软件(美国Origin Lab公司)进行模型拟合和回归分析。
1.5.1 一级模型
一级模型主要描述在一定环境条件下微生物数量随时间变化的关系[10]。本研究采用食品微生物领域较为常用的模型进行拟合,即修正的Gompertz模型、修正的Logistic模型和Baranyi模型[11]。
1.5.1.1 修正的Gompertz模型
修正的Gompertz模型属于经验模型,其模型表达式为[12]:
式(1)中:t为贮藏时间/d;N(t)为t时的微生物数量(lg(CFU/g));Nmax为微生物生长达到稳定期时的最大微生物数量(lg(CFU/g));N0为时间无限趋近于0时的微生物数量,相当于初始微生物数量(lg(CFU/g));μmax为微生物生长的最大比生长速率/d-1;λ为微生物生长的延滞时间/d。
1.5.1.2 修正的Logistic模型
修正的Logistic模型表达式为[13]:
式(2)中:u为在t=M时的相对最大生长速率/d-1;M为达到相对最大生长速率所需要的时间/d;其余各参数与式(1)中相同。其中μmax、λ与u、M的关系为:μmax=u(Nmax-N0)/4,λ=M-2/u。
1.5.1.3 Baranyi模型
Baranyi模型属于机械模型,其模型表达式为[14]:
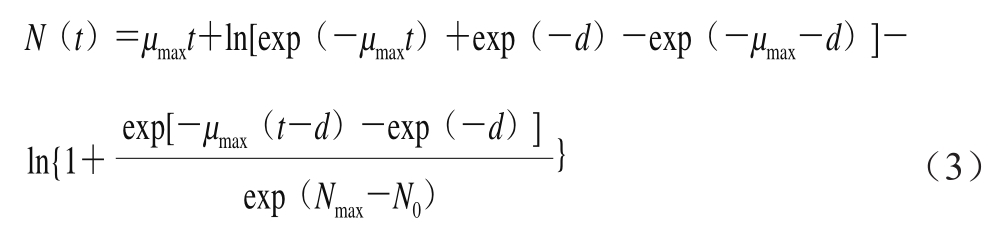
式(3)中:d为最大比生长速率μmax与延滞时间λ的乘积,其余各参数与式(1)中相同。
1.5.2 二级模型
二级模型表达的是一级模型中各生长参数与环境因素之间的关系,其中温度是最重要的环境因素[15]。本研究采用平方根模型(Belehradck model)和阿留尼乌斯模型(Arrhenius model)进行数据拟合。
1.5.2.1 Belehradck模型
Belehradck模型的表达式分别为[16]:
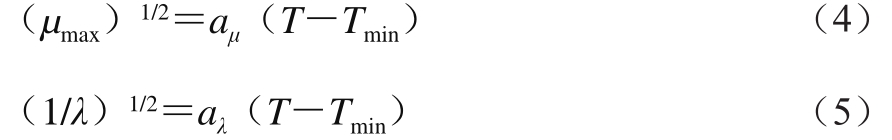
式(4)和(5)中:aμ和aλ为方程常数;T为贮藏温度/℃;Tmin为微生物最低生长温度/℃,这是一个假定概念,认为在此温度下微生物停止代谢活动或最大比生长速率为0 d-1。
1.5.2.2 Arrhenius模型
Arrhenius模型的表达式分别为[17]:
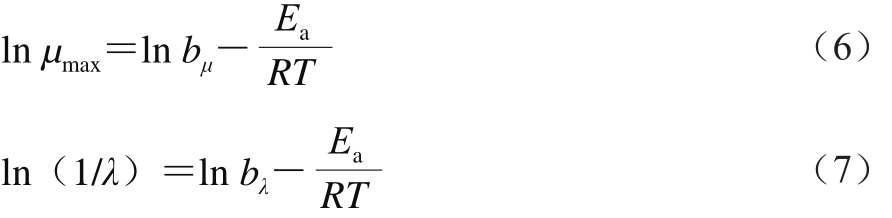
式(6)和(7)中:bμ和bλ为方程常数;Ea为活化能/(kJ/mol);R为气体常数,其值为8.314 J/(mol·K);T为开氏温度/K。
1.5.3 模型拟合效果的评价
使用回归相关系数R2、RMSE、AIC与BIC来比较微生物生长预测模型的拟合优度,从而评价不同模型的拟合效果,其中R2越接近于1,RMSE、AIC与BIC值越小,说明模型的拟合优度越高[18]。各评价参数的表达式分别为:
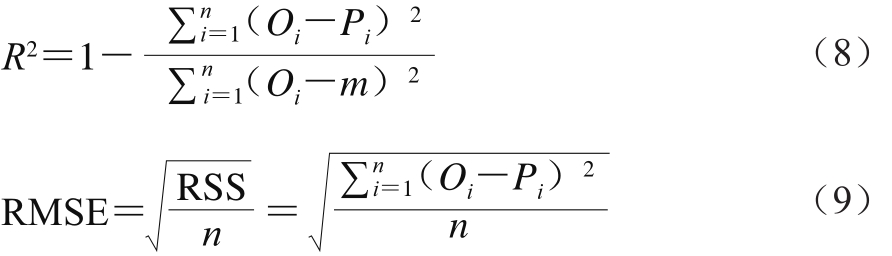
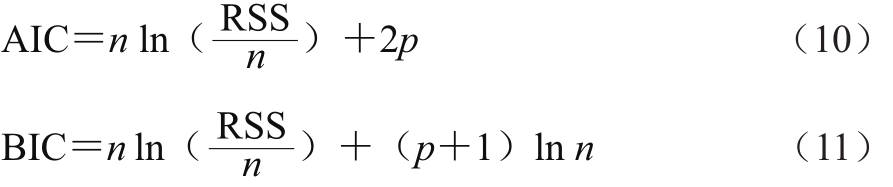
式(8)、(9)、(10)和(11)中:n为数据点个数;Oi为第i个数据点的实测值;Pi为第i个数据点的预测值;m为平均值;RSS为残差平方和;p为自变量个数。
1.5.4 模型的验证
1.5.4.1 一级模型的验证
使用偏差因子(bias factor,Bf)和准确因子(accuracy factor,Af)来验证一级模型的可靠性。其中,Bf用来衡量预测值是否高于或低于实测值,一般认为该值在0.75~1.25之间模型可被接受;Af用来衡量预测值与实测值之间的平均误差,一般认为该值在1.1~1.9之间模型可被接受。其表达式分别为[19]:

式(12)和(13)中:N预测为通过微生物生长预测模型得到的菌落总数(lg(CFU/g));N实测为实际测得的菌落总数(lg(CFU/g));n为数据点个数。
1.5.4.2 二级模型的验证
使用残差值对二级模型进行验证,其表达式为:

图1 不同贮藏温度下低温杀菌黄焖鸡中菌落总数的变化
Fig. 1 Changes in aerobic bacterial count of pasteurized braised chicken during storage at different temperatures
由图1可知,不同贮藏温度条件下,黄焖鸡中的菌落总数均随贮藏时间延长而增加,其中4 ℃贮藏条件下,黄焖鸡中菌落总数的变化最为缓慢,其在贮藏第0~42天有明显的延滞期,直到贮藏第56天菌落总数才有较为明显的增加(P<0.05)。同一贮藏期内,贮藏于15、25 ℃条件下的黄焖鸡中菌落总数明显高于4 ℃条件下贮藏的样品,这说明贮藏温度对产品的贮藏特性有重要影响,低温能够明显抑制黄焖鸡中微生物的生长[20]。根据GB 2726—2016《食品安全国家标准 熟肉制品》[21]中的规定,产品菌落总数的限量为5×104 CFU/g(即4.699 (lg(CFU/g))),因此,在4、15、25 ℃条件下贮藏的低温杀菌黄焖鸡分别于第140、28、6天超过安全标准。
表1 不同一级模型拟合所得的生长参数值
Table 1 Parameter eigenvalues of different primary models used to fit the experimental data
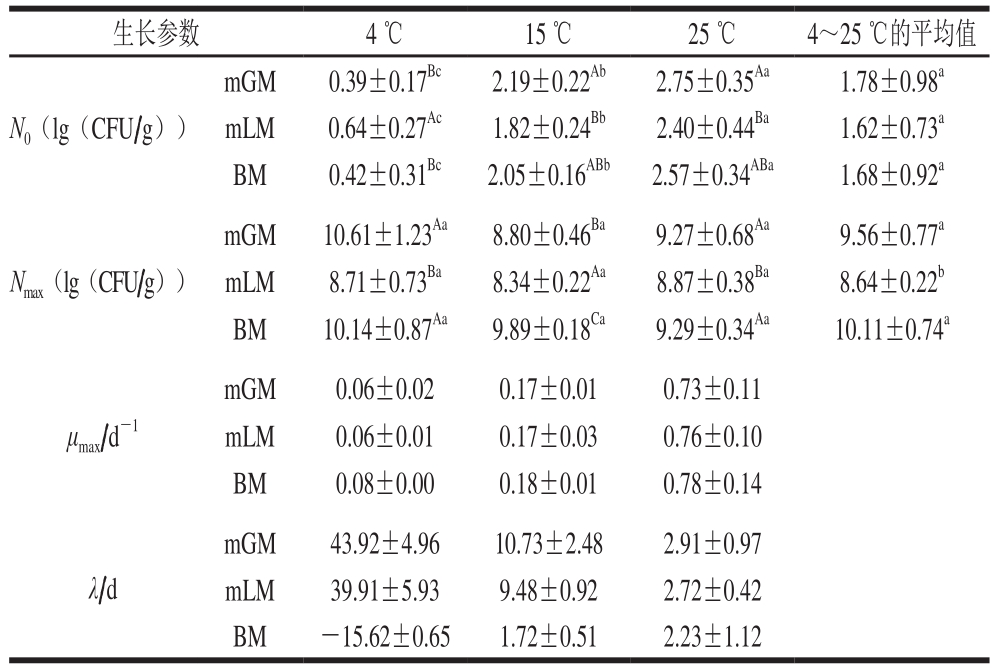
注:mGM. 修正的Gompertz模型;mLM. 修正的Logistic模型;BM.Baranyi模型;大写字母不同,表示不同模型在相同贮藏温度下拟合所得的同一参数值存在显著性差异(P<0.05);小写字母不同,表示相同模型在不同贮藏温度下拟合所得的同一参数值存在显著性差异(P<0.05)。
生长参数 4 ℃ 15 ℃ 25 ℃ 4~25 ℃的平均值N0(lg(CFU/g))mGM 0.39±0.17Bc 2.19±0.22Ab 2.75±0.35Aa 1.78±0.98a mLM 0.64±0.27Ac 1.82±0.24Bb 2.40±0.44Ba 1.62±0.73a BM 0.42±0.31Bc 2.05±0.16ABb 2.57±0.34ABa 1.68±0.92a Nmax(lg(CFU/g))mGM 10.61±1.23Aa 8.80±0.46Ba 9.27±0.68Aa 9.56±0.77a mLM 8.71±0.73Ba 8.34±0.22Aa 8.87±0.38Ba 8.64±0.22b BM 10.14±0.87Aa 9.89±0.18Ca 9.29±0.34Aa 10.11±0.74a μmax/d-1 mGM 0.06±0.02 0.17±0.01 0.73±0.11 mLM 0.06±0.01 0.17±0.03 0.76±0.10 BM 0.08±0.00 0.18±0.01 0.78±0.14 mGM 43.92±4.96 10.73±2.48 2.91±0.97 mLM 39.91±5.93 9.48±0.92 2.72±0.42 BM -15.62±0.65 1.72±0.51 2.23±1.12 λ/d
由表1可知,3 个模型拟合所得N0的平均值相差不大,而mLM拟合所得Nmax的平均值则显著小于mGM与BM(P<0.05),并且与实测值(7.75 (lg(CFU/g)))最接近。在不同贮藏温度下,mGM与mLM拟合所得的μmax更接近,均小于BM,这是由于mGM与mIM在描述微生物生长由延滞期进入对数期时函数图像的拐点相对平滑,导致计算出的μmax偏小[22]。3 个模型拟合所得的λ差异较大,其中BM将4 ℃贮藏组的λ计算为负值,这与陈鹏等[23]的研究结果相似,由于λ不可能为负数,因此使用BM拟合失败。
表2 不同一级模型拟合结果的评价指标
Table 2 Evaluation indexes of different primary models used to fit the experimental data
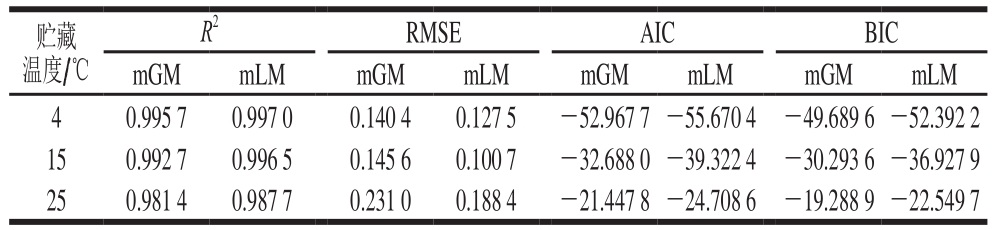
贮藏温度/℃R2 RMSE AIC BIC mGM mLM mGM mLM mGM mLM mGM mLM 4 0.995 7 0.997 0 0.140 4 0.127 5 -52.967 7-55.670 4 -49.689 6-52.392 2 15 0.992 7 0.996 5 0.145 6 0.100 7 -32.688 0-39.322 4 -30.293 6-36.927 9 25 0.981 4 0.987 7 0.231 0 0.188 4 -21.447 8-24.708 6 -19.288 9-22.549 7
由于BM拟合失败,因此对模型拟合效果的比较主要针对mGM和mLM。由表2可知,与mGM相比,相同贮藏温度条件下,mLM拟合结果的R2值更接近于1,且RMSE、AIC和BIC值均更小,说明在这2 种一级模型中,mLM的拟合优度较高,因此选用mLM来描述低温杀菌黄焖鸡在4、15、25 ℃贮藏期间的微生物生长情况更为合适。

图2 修正的Logistic模型拟合菌落总数在不同温度下的生长曲线
Fig. 2 Growth kinetic curves of aerobic bacterial count at different temperatures fitted with modified Logistic model
由图2可知,在4、15、25 ℃贮藏温度条件下,拟合曲线的形态有所差异。随着贮藏温度的升高,μmax逐渐增大,λ逐渐减小,在生长动力学意义上表示降低贮藏温度使微生物生长的最大比生长速率减小,延滞时间增加,这是由于低温可显著抑制微生物的增殖速率[24]。此外,温度对低温杀菌黄焖鸡贮藏期间的最大微生物数量Nmax无显著影响。上述模型参数分析结果与直观分析结果具有一致性。
表3 不同二级模型拟合结果的评价指标
Table 3 Evaluation indexes of different secondary models used to fit the experimental data
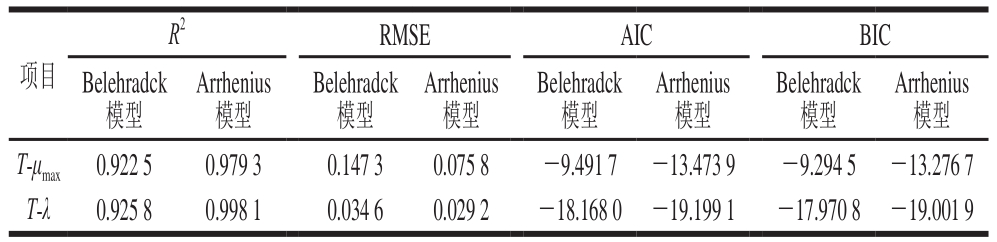
注:T-μmax和T-λ分别表示贮藏温度与最大比生长速率μmax和延滞时间λ之间的关系。
Arrhenius模型T-μmax 0.922 5 0.979 3 0.147 3 0.075 8 -9.491 7 -13.473 9 -9.294 5 -13.276 7 T-λ 0.925 8 0.998 1 0.034 6 0.029 2 -18.168 0 -19.199 1 -17.970 8 -19.001 9项目R2 RMSE AIC BIC Belehradck模型Arrhenius模型Belehradck模型Arrhenius模型Belehradck模型Arrhenius模型Belehradck模型
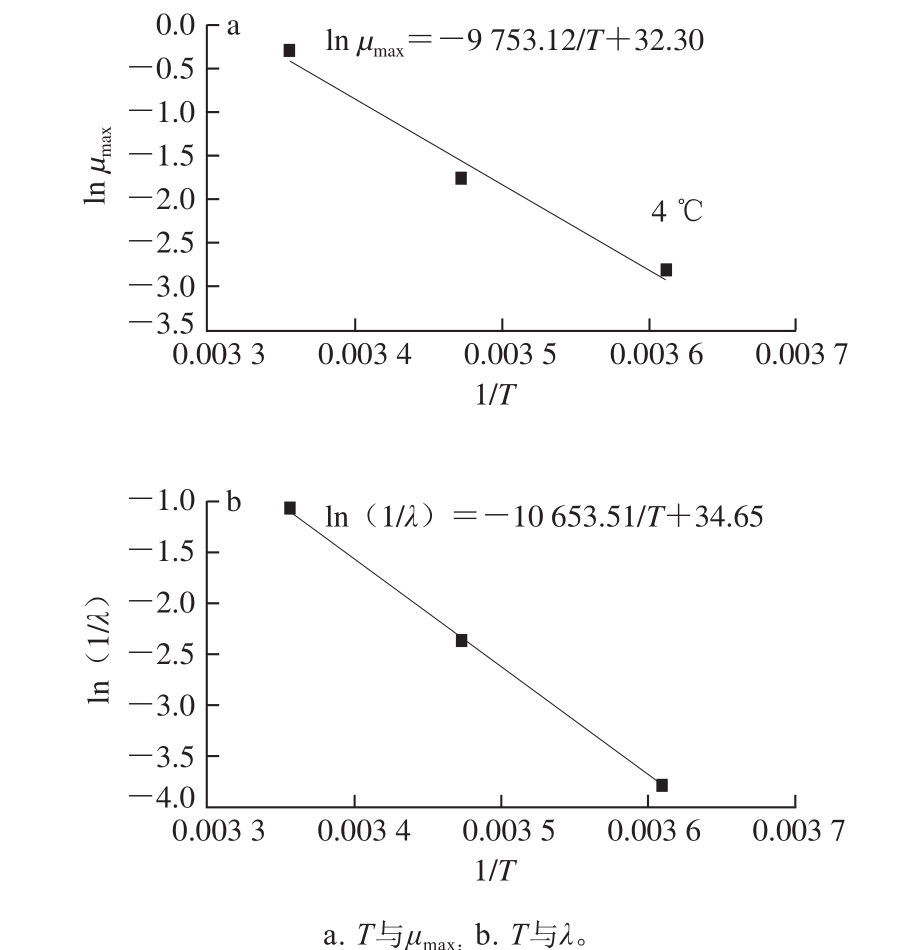
图3 温度与最大比生长速率μmax及延滞时间λ的关系
Fig. 3 Relationship between temperature and maximum specific growth rate μmax and lag phase λ
使用Belehradck模型和Arrhenius模型对一级模型所得的生长参数值进行拟合,计算模型的评价指标。由表3可知,与Belehradck模型相比,Arrhenius模型拟合所得结果的R2更接近于1,且RMSE、AIC和BIC值均小于Belehradck模型的拟合结果,说明在这2 种二级模型中,Arrhenius模型的拟合优度较高,该模型能够更好地描述低温杀菌黄焖鸡中菌落总数生长参数与温度之间的关系。
将一级模型求得的各温度条件下的μmax和λ拟合到Arrhenius模型中,得到拟合曲线及数学方程式。由图3可知,贮藏温度与μmax和λ 2 个参数之间均呈现良好的线性关系,随着贮藏温度的升高,μmax不断增大,λ不断减小,菌落总数达到最大值所需的时间不断减少,这与一级模型的拟合结果具有一致性。
表4 不同温度下菌落总数的修正Logistic模型Bf和Af
Table 4 Bf and Af of modified Logistic model for aerobic bacterial count at different temperatures

温度/℃ 实验次数(n) Bf Af 4 14 1.033 4 1.440 3 15 9 1.000 5 1.248 9 25 8 1.000 0 1.297 3
为验证建立的微生物生长预测模型的可靠性,本研究以4、15、25 ℃温度条件下菌落总数生长的实测值对最优一级模型(修正的Logistic模型)的准确性进行验证。由表4可知,计算得到的Bf在1.0左右,Af在1.2~1.5之间,均在可接受范围内,因此上述温度下建立的一级模型可被接受。
表5 不同温度下菌落总数生长参数的实测值、预测值及残差值
Table 5 Observed and predicted values and residual values of parameter eigenvalues at different temperatures
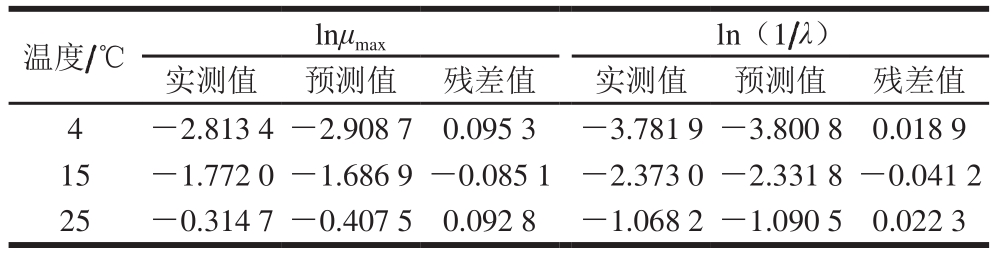
温度/℃ lnμmax ln(1/λ)实测值 预测值 残差值 实测值 预测值 残差值4 -2.813 4-2.908 7 0.095 3 -3.781 9-3.800 8 0.018 9 15 -1.772 0-1.686 9-0.085 1 -2.373 0-2.331 8-0.041 2 25 -0.314 7-0.407 5 0.092 8 -1.068 2-1.090 5 0.022 3
将菌落总数生长参数值与最优二级模型(Arrhenius模型)拟合得到的参数预测值进行比较,验证二级模型的可靠性。由表5可知,菌落总数在3 个温度条件下μmax与λ残差值的绝对值均小于0.1,在可接受范围内,因此上述温度条件下建立的二级模型可被接受。
由表1可知,菌落总数的初始值N0和最大值Nmax,利用修正的Logistic模型,变形得到低温杀菌黄焖鸡货架期预测模型的表达式为[25]:
式(15)中:SL为产品的货架期/d;Nmaxa为各温度条件下样品中最大菌落数的平均值(lg(CFU/g));Ns为腐败限量(lg(CFU/g))。
由于μmax和λ可以用Arrhenius模型进行预测,因此用图3中的温度表达式对μmax和λ进行替换。同时根据国家标准的规定可知,产品的腐败限量为4.699 (lg(CFU/g)),由此得出低温杀菌黄焖鸡在4~25 ℃范围内的货架期预测模型为:
表6 不同温度条件下低温杀菌黄焖鸡货架期的实测值、预测值及相对误差
Table 6 Observed and predicted shelf-life of pasteurized braised chicken stored at different temperatures

温度/℃ 实测值/d 预测值/d 相对误差/%4 140 128.24 -8.41 15 28 27.25 -2.66 25 6 5.71 -4.85
对低温杀菌黄焖鸡在4、15、25 ℃条件下货架期的预测值和实测值进行比较,计算相对误差值,验证模型的准确性。由表6可知,预测值和实测值的相对误差分别为-8.41%、-2.66%和-4.85%,均在±10%的范围内,说明此模型能够比较准确地预测黄焖鸡在4~25 ℃范围内的货架期,基于修正的Logistic模型和Arrhenius模型建立的货架期预测模型可被接受。
微生物生长预测模型种类繁多,因此比较不同模型的拟合优度,对于评价模型的拟合效果、建立准确可靠的产品货架期预测模型十分重要。本研究对于低温杀菌黄焖鸡贮藏期间菌落总数的变化情况进行研究,经分析后认为一级模型中修正的Logistic模型的拟合优度最高,其次为修正的Gompertz模型,Baranvi模型拟合失败;在二级模型中,Belehradck模型与Arrhenius模型均能成功拟合,但Arrhenius模型的评价指标更优,模型的拟合效果更好。许多学者对肉及肉制品中菌落总数生长预测模型的拟合效果进行了评价,例如:陈睿[26]描述了真空包装鸡肉早餐肠中菌落总数的生长情况,结果表明,在一级模型中,Baranyi模型的拟合优度最高,二级模型未能得出拟合更优者;丁婷等[27]研究发现,修正的Gompertz模型的拟合效果优于修正的Logistic模型和Baranyi模型,Belehradck模型和Arrhenius模型均能成功描述冷藏三文鱼片中菌落总数生长参数与贮藏温度间的关系。目前研究普遍认为,在一级模型中,修正的Gompertz模型和Baranyi模型的拟合优度较高,而二级模型中Belehradek模型和Arrhenius模型的比较结果存在差异,与本研究结论不一致,这可能与食品基质及环境特性等因素相关。
事实上,除了上述因素外,微生物种类也会对模型的建立和比较产生重要影响。由于肉及肉制品的腐败过程往往由多种微生物共同参与,菌落总数是最常选取的建模指标,它能够反映微生物之间相互作用的影响。近年来,许多学者开始将研究的目光转向特定腐败菌(specific spoilage organism,SSO),根据SSO的生长情况建立微生物生长预测模型,并结合品质指标建立低温杀菌肉制品的货架期预测模型,能够更有针对性地指导该类产品的实际生产和贮藏销售。Mathias等[28]以低温杀菌火鸡肉中的特定腐败菌乳酸菌为研究对象,建立其生长预测模型,并对产品的货架期进行预测;Yoon等[29]通过分析低温杀菌火腿中常见微生物与硫代巴比妥酸反应物值、pH值和感官评分等品质指标之间的相关性,确定单增李斯特菌为优势微生物,并建立其生长预测模型及产品的货架期预测模型;胡聪[30]建立了低温杀菌牛羊肉产品(卤牛肚、手抓羊肉)中假单胞菌的生长预测模型,并结合总挥发性盐基氮含量、pH值和失水率等品质指标建立了产品的货架期预测模型。因此在后续研究中,可以通过实验确定低温杀菌黄焖鸡中的特定腐败菌,并结合相关品质指标进一步完善产品的货架期预测模型,为低温杀菌黄焖鸡的微生物安全性研究和货架期预测提供数据支持,同时也为同类型产品的相关研究提供参考。
本研究针对低温杀菌黄焖鸡中菌落总数的生长情况,以拟合参数值和模型评价指标(R2、RMSE、AIC、BIC)为参考,对不同微生物生长预测模型的拟合效果进行比较,并选取最优模型组合,建立产品的货架期预测模型,结果表明:修正的Logistic模型是拟合优度最高的一级模型,该模型所得的生长参数值与实测值最接近,且模型的评价指标最优;在二级模型中,Arrhenius模型能更好地描述温度与一级模型所得生长参数之间的关系,模型的R2均在0.97以上;经过验证,修正的Logistic模型和Arrhenius模型可被接受;在此基础上建立低温杀菌黄焖鸡的货架期预测模型,模型的预测值和实测值的相对误差均在±10%范围内。因此,本研究基于修正的Logistic模型和Arrhenius模型建立的货架期预测模型能够比较准确地预测低温杀菌黄焖鸡在4~25 ℃范围内的货架期。
[1] 卢君逸, 罗瑞明, 刘莹莹, 等. 五香牛肉品质变化及安全贮藏期的界定研究[J]. 安徽农业科学, 2013, 41(11): 5034-5036. DOI:10.3969/j.issn.0517-6611.2013.11.118.
[2] BATT C A, TORTORELLO M L. Encyclopedia of food microbiology[M]. 2nd ed. Manhattan: Academic Press, 2014: 59-68.
[3] 金鑫, 周光宏, 徐幸莲, 等. 预测食品微生物学在肉品安全领域的应用[J]. 肉类研究, 2010, 24(7): 3-7.
[4] DELHALLE L, DAUBE G, ADOLPHE Y, et al. A review of growth models in predictive microbiology to ensure food safety[J].Biotechnology, Agronomy, Society and Environment, 2012, 16(3):369-381. DOI:10.1080/10889868.2012.687417.
[5] 陈睿, 徐幸莲, 周光宏, 等. 真空包装鸡肉早餐肠中细菌总数生长预测模型的拟合优度比较[J]. 食品科学, 2014, 35(15): 113-117.DOI:10.7506/spkx1002-6630-201415023.
[6] 朱彦祺, 郭全友, 李保国, 等. 不同温度下腐败希瓦氏菌(Shewanella putrefaciens)生长动力学模型的比较与评价[J]. 食品科学, 2016,37(13): 147-152. DOI:10.7506/spkx1002-6630-201613026.
[7] YANG S, PARK S Y, HA S D. A predictive growth model of Aeromonas hydrophila on chicken breasts under various storage temperatures[J]. LWT-Food Science and Technology, 2016, 69:98-103. DOI:10.1016/j.lwt.2016.01.016.
[8] 常思盎, 惠腾, 刘毅, 等. 杀菌和复热工艺对黄焖鸡挥发性风味物质的影响[J]. 肉类研究, 2018, 32(4): 20-26. DOI:10.7506/rlyj1001-8123-201804004.
[9] 中华人民共和国国家卫生和计划生育委员会, 国家食品药品监督管理总局. 食品安全国家标准 食品微生物学检验 菌落总数测定:GB 4789.2—2016[S]. 北京: 中国标准出版社, 2016.
[10] 张昭寰, 娄阳, 杜苏萍, 等. 分子生物学技术在预测微生物学中的应用与展望[J]. 食品科学, 2017, 38(9): 248-257. DOI:10.7506/spkx1002-6630-201709040.
[11] YE Keping, WANG Huhu, ZHANG Xinxiao, et al. Development and validation of a molecular predictive model to describe the growth of Listeria monocytogenes in vacuum-packaged chilled pork[J]. Food Microbiology, 2013, 32(1): 246-254. DOI:10.1016/j.foodcont.2012.11.017.
[12] GONZÁLEZ-FANDOS E, GARCÍA-LINARES M C, VILLARINORODRÍGUEZ A, et al. Evaluation of the microbiological safety and sensory quality of rainbow trout (Oncorhynchus mykiss) processed by the sous vide method[J]. Food Microbiology, 2004, 21(2): 193-201.DOI:10.1016/S0740-0020(03)00053-4.
[13] SAITO K, JIN D H, OGAWA T, et al. Antioxidative properties of tripeptide libraries prepared by the combinatorial chemistry[J].Journal of Agricultural and Food Chemistry, 2003, 51(12): 3668-3674.DOI:10.1021/jf021191n.
[14] BARANYI J, ROBERTS T A. A dynamic approach to predicting bacterial growth in food[J]. International Journal of Food Microbiology, 1994, 23(3/4): 277-294. DOI:10.1016/0168-1605(94)90157-0.
[15] KREYENSCHMIDT J, CHRISTIANSEN H, ALBRECHT A, et al.A novel photochromic time-temperature indicator to support cold chain management[J]. International Journal of Food Microbiology, 2010,45(2): 208-215. DOI:10.1111/j.1365-2621.2009.02123.x.
[16] HONG Y K, HUANG L H, YOON W B. Mathematical modeling and growth kinetics of Clostridium sporogenes in cooked beef[J]. Food Control, 2016, 60(7): 471-477. DOI:10.1016/j.foodcont.2015.08.035.
[17] 李秋庭, 吴建文. 盐焗鸡贮藏品质变化及货架期预测模型[J]. 食品科技, 2015, 40(2): 157-162. DOI:10.13684/j.cnki.spkj.2015.02.033.
[18] FENG C H, DRUMMOND L, SUN D W, et al. Modeling the growth parameters of lactic acid bacteria and total viable count in vacuumpackaged Irish cooked sausages cooled by different methods[J].International Journal of Food Science and Technology, 2014, 49(12):2659-2667. DOI:10.1111/ijfs.12603.
[19] 姜颖. 真空包装烤肠货架期预测及保鲜技术研究[D]. 北京: 中国农业科学院, 2016: 19-32.
[20] DURACK E, ALONSO-GOMEZ M, WILKINSON M G. The effect of thawing and storage temperature on the microbial quality of commercial frozen ready meals and experimental reduced salt frozen ready meals[J]. Journal of Food Research, 2012, 1(2): 99-112.DOI:10.5539/jfr.v1n2p99.
[21] 中华人民共和国国家卫生和计划生育委员会, 国家食品药品监督管理总局. 食品安全国家标准 熟肉制品: GB 2726—2016[S]. 北京:中国标准出版社, 2016.
[22] 陈睿, 徐幸莲, 周光宏. 真空包装鸡肉早餐肠货架期预测模型的建立[J]. 食品科学, 2014, 35(6): 209-213. DOI:10.7506/spkx1002-6630-201406045.
[23] 陈鹏, 程镜蓉, 杨禹新, 等. 冷鲜黄羽肉鸡货架期预测模型的建立与评价[J]. 食品工业科技, 2016, 37(12): 144-148. DOI:10.13386/j.issn1002-0306.2016.12.020.
[24] 胡洁云, 林露, 王彤, 等. 熟鸡肉中金黄色葡萄球菌生长预测模型的建立[J]. 微生物学通报, 2016, 43(9): 1999-2009. DOI:10.13344/j.microbiol.china.150738.
[25] 张婉. 鲜熟面贮藏品质及货架期预测模型研究[D]. 烟台: 烟台大学,2012: 23-29.
[26] 陈睿. 真空包装鸡肉早餐肠腐败进程分析及货架期预测模型研究[D].南京: 南京农业大学, 2014: 47-56.
[27] 丁婷, 李婷婷, 励建荣, 等. 冷藏三文鱼片微生物生长动力学模型适用性分析及货架期模型的建立[J]. 中国食品学报, 2015, 15(5):63-73. DOI:10.16429/j.1009-7848.2015.05.009.
[28] MATHIAS S P, ROSENTHAL A, GASPAR A, et al. Prediction of acid lactic-bacteria growth in turkey ham processed by high hydrostatic pressure[J]. Brazilian Journal of Microbiology, 2013, 44(1): 23-28.DOI:10.1590/S1517-83822013005000014.
[29] YOON Y, GEOMARAS I, SCANGA G A, et al. Probabilistic models for the prediction of target growth interfaces of Listeria monocytogenes on ham and turkey breast products[J]. Journal of Food Science, 2011,76(6): 450-455. DOI:10.1111/j.1750-3841.2011.02273.x.
[30] 胡聪. 清真牛羊肉产品微生物预测软件开发[D]. 银川: 宁夏大学,2014: 21-38.
Goodness-of-fit Comparison of Prediction Models for Aerobic Bacterial Count and Shelf Life Prediction of Pasteurized Braised Chicken
常思盎, 刘毅, 邵乐乐, 等. 低温杀菌黄焖鸡中菌落总数生长预测模型的比较和货架期预测[J]. 肉类研究, 2019, 33(4):42-48. DOI:10.7506/rlyj1001-8123-20190304-047. http://www.rlyj.net.cn
CHANG Siang, LIU Yi, SHAO Lele, et al. Goodness-of-fit comparison of prediction models for aerobic bacterial count and shelf life prediction of pasteurized braised chicken[J]. Meat Research, 2019, 33(4): 42-48. DOI:10.7506/rlyj1001-8123-20190304-047.http://www.rlyj.net.cn