表1 L
9（3
4）正交试验因素与水平
Table 1 Factors and levels used in L
9(3
4) orthogonal array design
水平因素温度/℃a wpH 1 250.955.5 2 300.976.0 3 370.996.5
李金春，周 彤，李家鹏*，陈 曦，杨君娜，许随根，陈文华
（中国肉类食品综合研究中心，肉类加工技术北京市重点实验室，北京 100068）
摘 要：采用营养肉汤培养基，研究不同温度、pH值和水分活度对金黄色葡萄球菌生长规律的影响，并构建金黄色葡萄球菌菌落数的一级生长模型和最大比生长速率、延滞期的二级生长模型，其中一级模型通过Baranyi模型来拟合；二级模型包括单因素二级模型和多因素二级模型，分别通过Bĕlehrádek平方根模型和二次多项式回归模型来拟合。结果表明：金黄色葡萄球菌生长速率随着温度、pH值和水分活度的增加而增加，而延滞期随着温度、pH值和水分活度的增加而降低，并且温度与pH值，温度与水分活度以及pH值与水分活度之间存在明显的交互作用。一级Baranyi模型、二级平方根模型以及多项式回归模型拟合性较好（R 2＞0.85）。通过数学检验参数精确因子（A f）、偏差因子（B f）、均方根误差（RMSE）对模型进行数学检验，表明构建的一级、二级模型适用性、可靠性和拟合性均在可接受范围内，在建模设定的范围内能预测金黄色葡萄球菌建模范围内的延滞期和最大比生长速率。
关键词：金黄色葡萄球菌；营养肉汤；预测微生物学；生长模型
金黄色葡萄球菌（ Staphyloccocus aureus）是一种革兰氏染色阳性球型细菌，隶属于葡萄球菌属，除了常引起皮肤的化脓性炎症外，其产生的肠毒素可导致食物中毒，是近年来危害食品安全的食源性致病菌 [1]。近年来，国内外关于致病菌的生长模型、致死模型均有大量报道，致病菌主要包括沙门氏菌 [2-3]、单增李斯特菌 [4-6]、大肠杆菌O157∶H7 [7-9]、金黄色葡萄球菌等 [10-11]，其中对金黄色葡萄球菌的研究多集中于单一因素的一级和二级生长模型，多因素生长模型研究的相对较少 [12-14]。利用传统微生物方法对食品中金黄色葡萄球菌进行监测费时又费力。通过微生物预测技术对食品中的致病菌建立不同条件下的模型，然后根据模型对致病菌的生长和死亡规律进行分析预测，可提高效率、节约人力物力。预测微生物学 [15-16]是一门运用数学模型来描述和预测给定条件下食品中微生物生长、衰亡规律的新兴技术，目前已在食品风险评估和食品安全控制领域发挥着重要作用。Whiting等 [17]将模型划分3 个层次，一级模型描述的是微生物的生物量随着时间变化的函数关系，可得到延滞期、最大比生长速率以及最大菌落数，主要包括Baranyi、Logistic、Modifi ed-Gompertz等模型 [18]；二级模型描述的是一级模型中各参数（如最大比生长速率、延滞期等）与条件因素（如温度、pH值、水分活度等）之间的函数关系，上世纪八九十年代由Bĕlehrádek开创、Ratkowsky等改进的平方根模型在拟合不同温度或pH值下微生物的生长参数（最大比生长速率和迟滞期）是其中的典型代表 [19]。三级模型是以数学模型和参数数据库为基础编写的计算机程序或软件，主要包括PMP、FSP、ComBase等。
本实验通过研究营养肉汤培养基中金黄色葡萄球菌在pH值、水分活度（a w）和温度（T）3个因素影响下的生长规律，建立金黄色葡萄球菌菌落数的一级生长模型和最大比生长速率（μ max）、延滞期（Lag）的单因素、多因素二级生长模型，通过模型可以获得金黄色葡萄球菌在建模范围内的μ max和Lag，从而预测其生长情况，为完善致病微生物预测技术提供数据支持。
1.1 菌种、材料与试剂
金黄色葡萄球菌（ Staphylococcus aureus ，ATCC 27217），由北京市食品质量监督检验三站提供。菌种采用磁珠法在―80 ℃低温保藏。
营养肉汤（NB）、胰蛋白胨大豆肉汤（TSB）、平板计数琼脂（PCA） 北京陆桥技术有限责任公司；乳酸、氯化钠 国药集团化学试剂有限公司；菌种保藏试剂盒 友康恒业生物科技有限公司。
1.2 仪器与设备
BT224S型分析天平 赛多利斯科学仪器（北京）有限公司；F1-45 Toyo型恒温培养箱 东洋化学产业有限公司；GI54DWS型全自动高压灭菌器 美国致微（厦门）仪器有限公司；ESCO型二级生物安全柜 上海金鹏分析仪器有限公司；FSP-625型匀浆机 日本Nihonseiki Kaisha公司；PHT-810型pH测量仪 广州市毅佰科学仪器有限公司；Labmaster型水分活度仪 瑞士Novasina公司。
1.3 方法
1.3.1 菌种活化、接种与计数
菌种活化：将菌种接种到10 mL TSB增菌液中进行活化，37 ℃、150 r/min振荡培养8 h，活化至对数初期（约10 5CFU/mL）。扩大培养：按0.5%的比例将活化好的菌种接种到100 mL TSB增菌液中进行扩大培养，30 ℃静态过夜培养至对数后期（约10 9CFU/mL），制得菌种原液。按照GB4789.10—2010《食品微生物检验 金黄色葡萄球菌检验》 [20]进行菌落计数。均做3 个平行，重复2 次。1.3.2 单因素试验
金黄色葡萄球菌的最适培养条件为温度37 ℃、pH 6.0、a w0.98。选择初始pH值（4.5、5.0、5.5、6.0、6.5）、a w（0.91、0.93、0.95、0.97、0.99）和培养温度（15、20、25、30、37 ℃）3 个因素进行单因素试验，考察各个因素对金黄色葡萄球菌生长的影响。其中水分活度通过NaCl溶液来调节 [21]，营养肉汤培养基中a w与NaCl溶液质量浓度符合二次函数关系：a w=―1.203x 2―0.348 4x＋0.987 2，式中：x为NaCl质量浓度/（g/mL）；pH值通过乳酸进行调节；根据菌种原液的浓度取适量接种到营养肉汤培养基中，使初始接种量在10 3CFU/mL左右，培养时间为24 h，在0、4、6、8、10、12、24 h时取样检测金黄色葡萄球菌菌落数（CFU/mL）。
1.3.3 正交试验
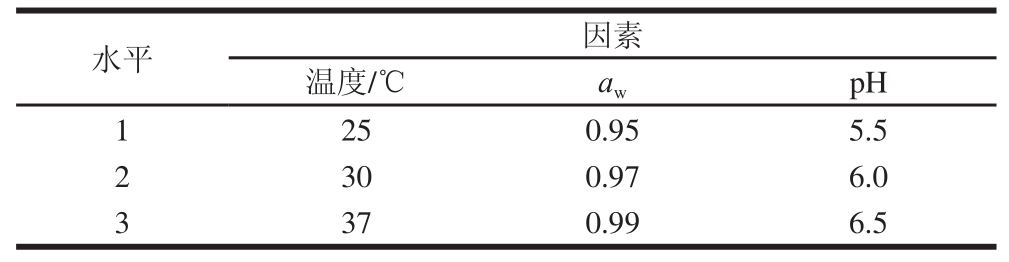
在单因素试验的基础上设计L 9（3 4）正交试验来研究pH值、a w和温度对金黄色葡萄球菌的综合生长作用。正交试验因素与水平如表1所示。培养时间为24 h，在0、4、6、8、10、12、24 h时取样检测金黄色葡萄球菌菌落数（CFU/mL）。
表1 L
9（3
4）正交试验因素与水平
Table 1 Factors and levels used in L
9(3
4) orthogonal array design
水平因素温度/℃a wpH 1 250.955.5 2 300.976.0 3 370.996.5
1.4 生长模型
1.4.1 一级Baranyi生长模型
根据单因素试验结果，建立pH值、a w、温度对金黄色葡萄球菌的Baranyi生长模型，采用Origin 8.0软件进行拟合，模型公式为 [22]：
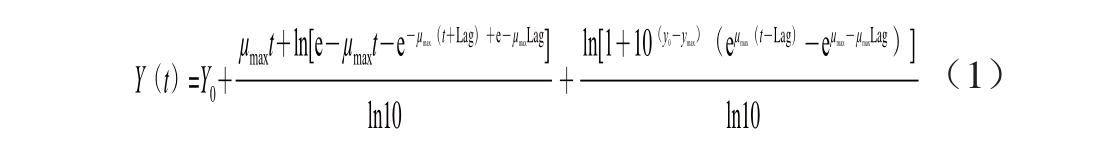
式中：Y（t）为t时刻样品中的微生物数量的自然对数（ln（CFU/g））；Y 0为初始时样品中的微生物细胞数量的自然对数（ln（CFU/g））；μ max为最大比生长速率/h －1；Lag为微生物延滯生长期的时间/h。
1.4.2 二级生长模型
1.4.2.1 单因素-Bĕlehrádek平方根模型
根据微生物在不同温度条件下，μ max或Lag倒数的平方根与温度之间存在的线性关系，得出了平方根经验 [19]模型，如公式（2）和（3）所示：
式中：T为温度/℃，适用范围是微生物最低生长温度到最适生长温度之间；T min μ、T min Lag均是假设的概念，指微生物没有代谢活动时对应的温度，是通过外推回归线与温度轴相交而得到的温度，即在此温度时微生物生长速率为零；b μ、b Lag分别是方程（2）和（3）的常数。Zwietering等 [23]提出pH值对微生物生长速率的影响可以用平方根经验模型（2）和（3）来描述，同样的a w对微生物速率的影响也可以用（2）和（3）来描述。
1.4.2.2 多因素多项式回归模型
根据正交试验的结果，通过二次多项式逐步回归的方法进行拟合，得到金黄色葡萄球菌μ max和Lag与温度、a w、pH值之间二次多项式。根据模型方程讨论了各个因素之间对金黄色葡萄球菌生长的交互作用。模型公式为 [24]：
式中：x 1为温度/℃；x 2为a w；x 3为pH值；p i（i=1，2，3，…，10）为多项式回归系数。
1.4.3 数学检验与评价
数学模型通常用精确因子（A f）、偏差因子（B f）、均方根误差（RMSE） [25]和决定系数（R 2）4个参数来评判拟合度的优劣。其中A f、B f和RMSE公式如下：
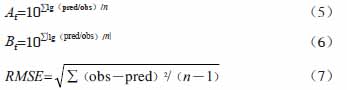
式中：n为实验中实测值的个数；pred为预测值；obs为实测值。
1.5 数据分析
用Origin 8.0软件进行单因素试验数据的处理、一级生长模型的构建以及柱形图绘制；用DPS 7.05软件对二级生长模型进行数据处理和模型的构建；用PASW Statistics 18.0软件进行pH值、a w和温度对金黄色葡萄球菌生长作用的显著性分析；通过Microsoft Excel 2007软件进行正交试验以及模型评价因子A f、B f、RMSE和R 2数据处理分析。
2.1 单因素试验
2.1.1 pH值对金黄色葡萄球菌生长的影响
金黄色葡萄球菌的最适生长pH值为7，pH值降低会抑制其生长。
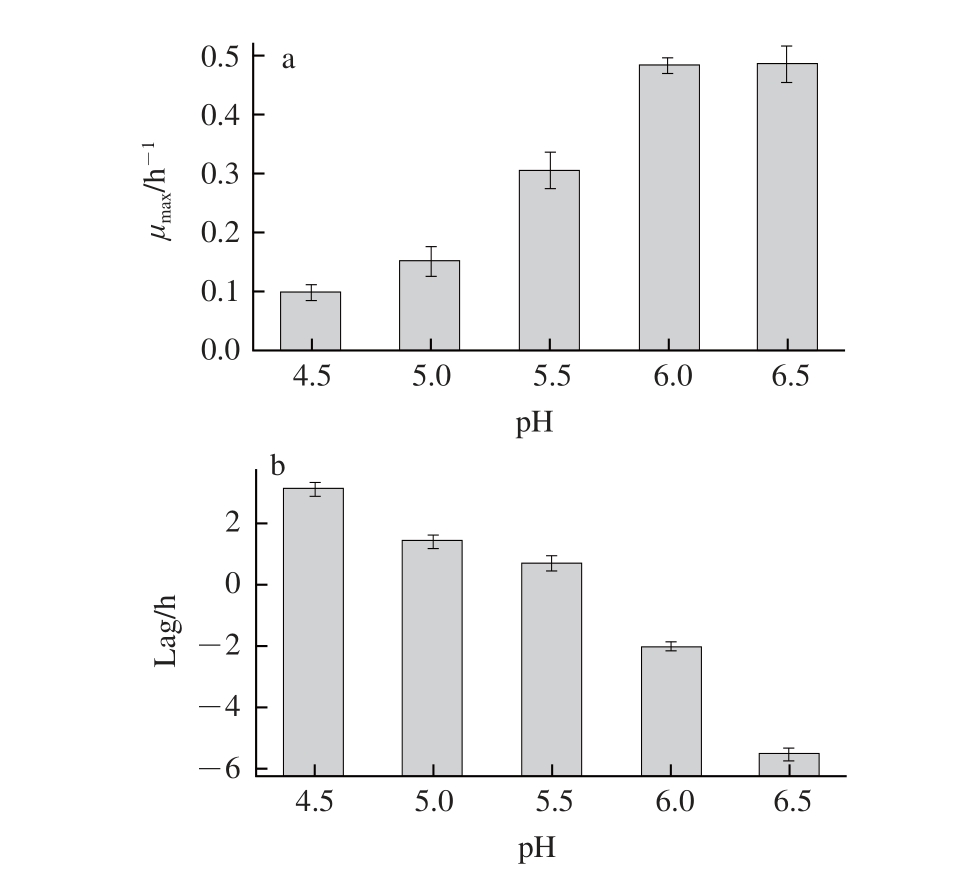
图1 pH值对金黄色葡萄球菌μ
max（a）和Lag（b）的影响
Fig.1 Effect of pH on the μ
max(a) and lag time (b) of
Staphylococcus aureus
由图1可知，pH值对金黄色葡萄球菌的μ max影响较大，pH值在4.0～6.0范围内金黄色葡萄球菌的μ max随着pH值的增加而显著增加（P＜0.05）。而当pH值大于6.0时，金黄色葡萄球菌的μ max趋于平稳。Stewart等 [26]研究了金黄色葡萄球菌的在不同pH值条件下的生长情况，发现pH值在3.0～7.0范围内随着pH值的增加，μ max先增加后趋于稳定，与本研究相一致。金黄色葡萄球菌的Lag值随pH值的增高而降低，随着pH值的增高，对金黄色葡萄球菌的抑制作用减弱，从而使Lag值逐渐减小。
2.1.2 a w对金黄色葡萄球菌生长的影响
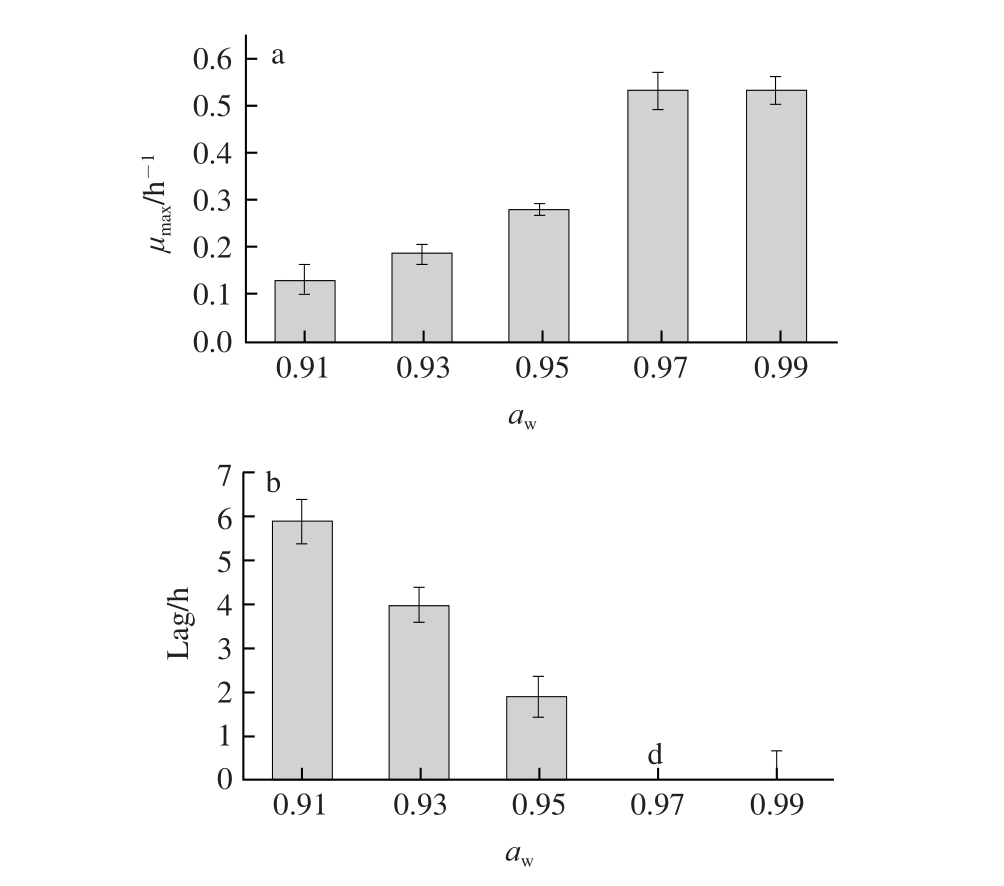
图2 a
w对金黄色葡萄球菌μ
max（a）和Lag（b）的影响
Fig.2 Effect of a
won the μ
max(a) and lag time (b) of
Staphylococcus aureus
金黄色葡萄球菌有高度的耐盐性，在15 g/100 mL NaCl溶液中都可以生长 [27]。营养肉汤培养基的a w通过NaCl溶液来调节，NaCl溶液质量浓度越高，a w越低。金黄色葡萄球菌最适生长a w为0.99。由图2可知，营养肉汤培养基中a w在0.91～0.97范围内，金黄色葡萄球菌μ max随着a w的增加而显著增加（P＜0.05）；a w大于0.97时，μ max趋于稳定。营养肉汤培养基中a w为0.91（NaCl溶液约为0.15 g/mL）时，金黄色葡萄球菌依然能够生长，说明金黄色葡萄球菌能够在低a w条件下生长。金黄色葡萄球菌的Lag值随a w的增高而降低。
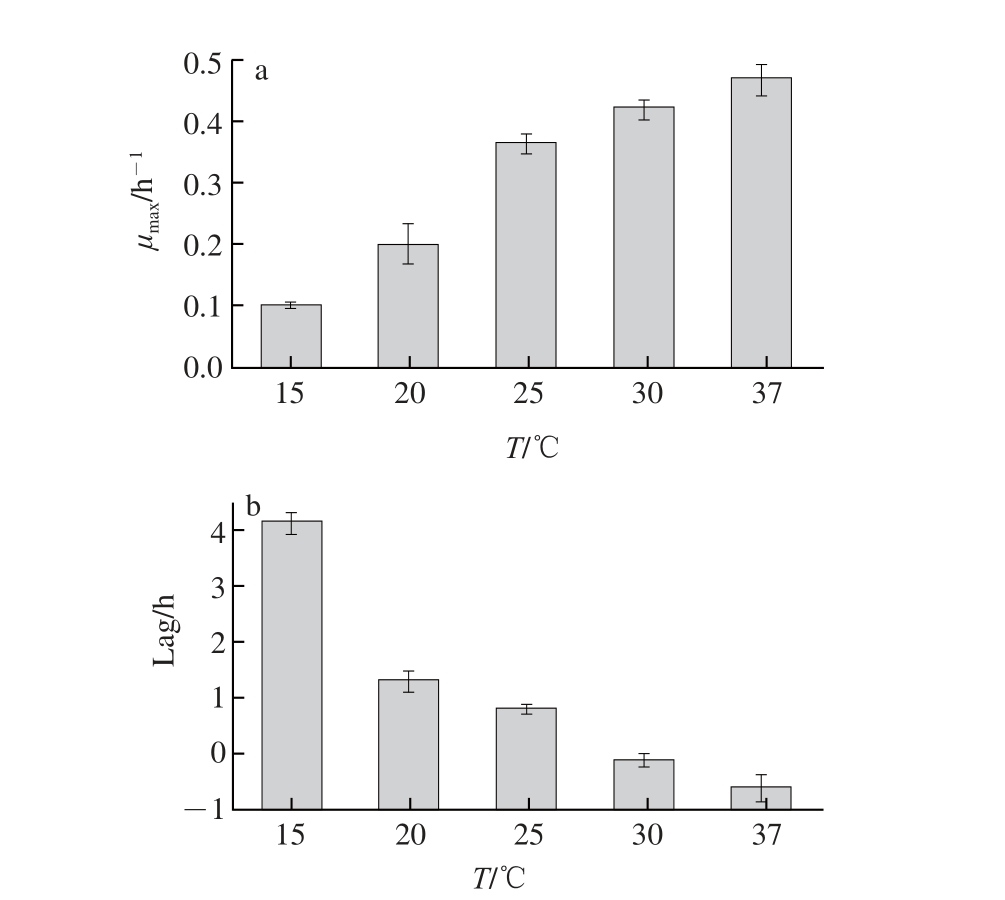
图3 温度对金黄色葡萄球菌μ
max（a）和Lag（b）的影响
Fig.3 Effect of temperature on the μ
max(a) and lag time (b) of
Staphylococcus aureus
2.1.3 温度对对金黄色葡萄球菌生长的影响金黄色葡萄球菌的最适生长温度为37 ℃。温度低于最适温度时，金黄色葡萄球菌的生长受到抑制。由图3可知，在15～37 ℃温度范围内，随着温度的增加金黄色葡萄球菌μ max显著增加（P＜0.05）。金黄色葡萄球菌的Lag
值随温度的增高而降低，随着温度的增高，对金黄色葡萄球菌的抑制作用减弱，从而使Lag逐渐减小。
2.2 正交试验
表2 L
9（3
4）正交试验结果
Table 2 Results of L
9(3
4) orthogonal array design
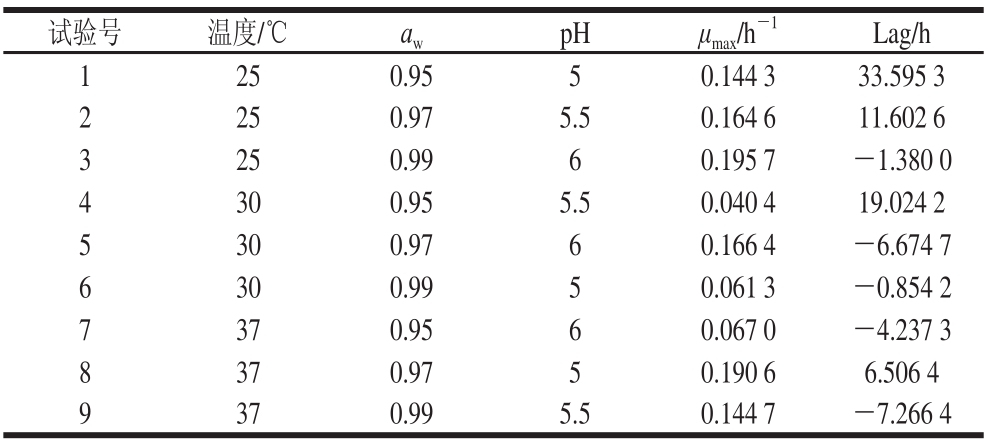
试验号温度/℃a wpHμ max/h －1Lag/h 1 250.9550.144 333.595 3 2 250.975.50.164 611.602 6 3 250.9960.195 7－1.380 0 4 300.955.50.040 419.024 2 5 300.9760.166 4－6.674 7 6 300.9950.061 3－0.854 2 7 370.9560.067 0－4.237 3 8 370.9750.190 66.506 4 9 370.995.50.144 7－7.266 4
由表2可知，各因素不同水平的组合下，金黄色葡萄球菌的μ max均不相同，μ max的变化范围从0.060 4 h －1到0.195 7 h －1，分布比较均匀，有利于二级生长模型的建立。μ max最大值出现在第3组试验，当培养温度25 ℃、a w0.99、pH 6时，μ max为0.195 7 h －1。而最小μ max值出现在第4组试验，为0.040 4 h －1。金黄色葡萄球菌的Lag值在各因素不同水平的组合下分布比较均匀，亦有利于二级生长模型的建立。
2.3 一级Baranyi生长模型
一级模型描述的是微生物的生物量随着时间变化的函数关系，在此基础上可进一步计算出迟滞期、生长速率以及最大菌数，Baranyi模型是一级模型中的典型代表 [28]；Baranyi模型属于机理模型，是根据微生物的生长代谢机理推导出的动力学方程，该模型能够很好处理延滞生长期，能够用来拟合完整的“S”形曲线，不仅能描述生长曲线也能描述致死曲线，而且也能用于波动的环境。pH值、a w与温度对应的Baranyi模型各参数如表3所示，其中决定系数R 2均在0.98左右，说明Baranyi模型能够分别拟合不同pH值、a w与温度条件下金黄色葡萄球菌的生长规律。
表3 pH值、a w与T对应的Baranyi模型各参数
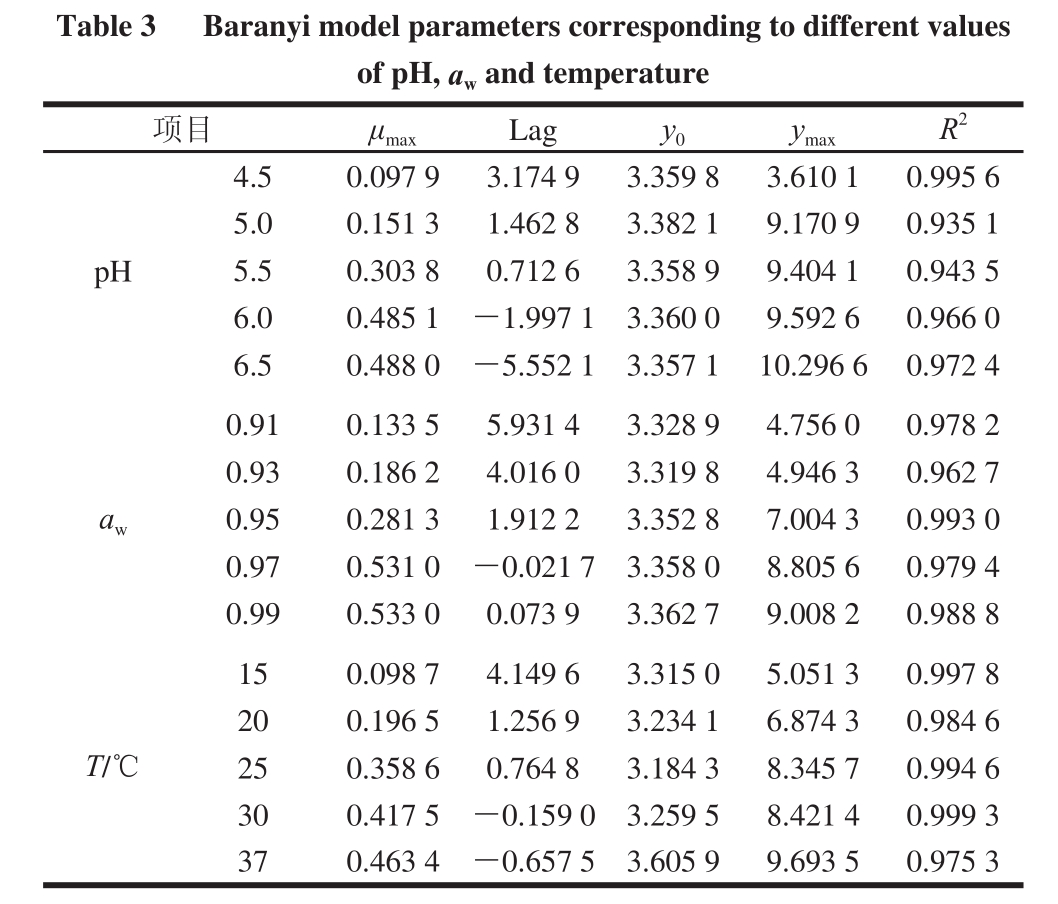
TTaabbllee 33 BBaarraannyyii mmooddeell ppaarraammeetteerrss ccoorrrreessppoonnddiinngg ttoo ddiiffffeerreenntt vvaalluueess of ppHH,, a wand temperatuurree项目μ maxLagy 0y maxR 2pH 4.50.097 93.174 93.359 83.610 10.995 6 5.00.151 31.462 83.382 19.170 90.935 1 5.50.303 80.712 63.358 99.404 10.943 5 6.00.485 1－1.997 13.360 09.592 60.966 0 6.50.488 0－5.552 13.357 110.296 60.972 4 aw 0.910.133 55.931 43.328 94.756 00.978 2 0.930.186 24.016 03.319 84.946 30.962 7 0.950.281 31.912 23.352 87.004 30.993 0 0.970.531 0－0.021 73.358 08.805 60.979 4 0.990.533 00.073 93.362 79.008 20.988 8 T/℃150.098 74.149 63.315 05.051 30.997 8 200.196 51.256 93.234 16.874 30.984 6 250.358 60.764 83.184 38.345 70.994 6 300.417 5－0.159 03.259 58.421 40.999 3 370.463 4－0.657 53.605 99.693 50.975 3
2.4 二级生长模型
2.4.1 单因素Bĕlehrádek平方根模型
表4 pH值、a w与T对应的Bĕlehrádek平方根模型
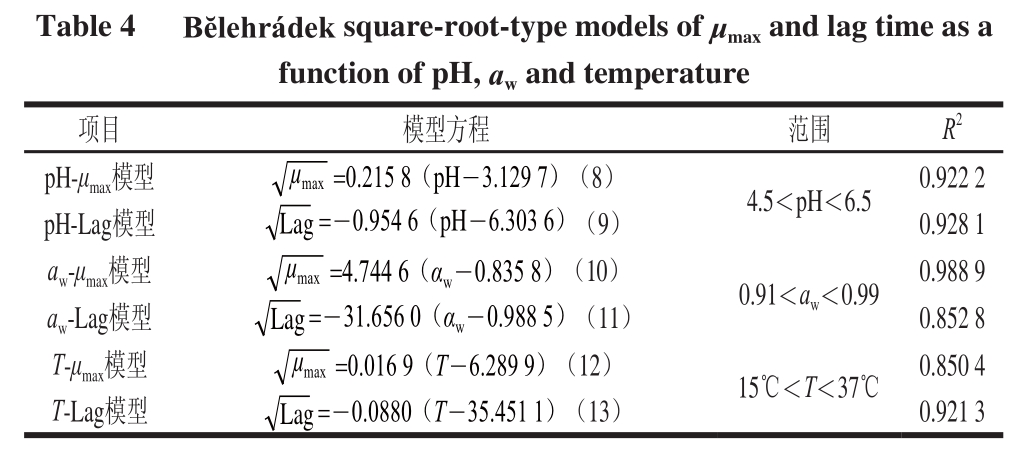
Tabllee 44 Bĕlehrráddeekk square-root-type models off μ
maxand lag time as a function of pHH,, a
wand temperatuurree项目模型方程范围R
2pH-μ
max模型（8）4.5＜pH＜6.50.922 2 pH-Lag模型
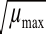μ
max=0.215 8（pH－3.129 7）
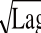=－0.954 6（pH－6.303 6）Lag（10）0.91＜a
w＜0.990.988 9 a
w-Lag模型（9）0.928 1 a
w-μ
max模型
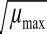μ
max=4.744 6（α
w－0.835 8）
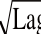=－31.656 0（α
w－0.988 5）Lag（12）15℃＜T＜37℃0.850 4 T-Lag模型（11）0.852 8 T-μ
max模型
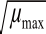μ
max=0.016 9（T－6.289 9）
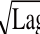=－0.0880（T－35.451 1）Lag （13）0.921 3
实验结果表明金黄色葡萄球菌生长速率随着温度、pH值和水分活度的增加而增加，而延滞期随着温度、pH值和水分活度的增加而降低，并且温度与pH值，温度与水分活度以及pH值与水分活度之间存在明显的交互作用。一级Baranyi模型、二级平方根模型以及多项式回归模型拟合性较好（R 2＞0.85），在建模设定的范围内能预测金黄色葡萄球菌建模范围内的延滞期和最大比生长速率。构建模型选取的温度、pH值和水分活度3 个因素与萨拉米香肠加工过程中发酵阶段的一些重要环境因素和栅栏因子存在一一对应关系，而各个模型均能够很好地预测金黄色葡萄球菌在营养肉汤中的最大比生长速率和延滞期，这为评估萨拉米香肠生产体系风险系数和制定产品质量安全控制方案提供重要参考依据。
参考文献：
[1] ZHANG Yanjun， ZHANG Junyan， MEI Lingling， et al. Typing and distribution of toxingenes among Staphylococcus aureusisolates from samples of milk[J]. Chinese Journal of Health Laboratory Technology，2005， 15(6): 682-683.
[2] THOMAS P， OSCAR I. Development and validation of a tertiary simulation model for predicting the potential growth of Salmonella typhimuriumon cooked chicken[J]. International Journal of Food Microbiology， 2002， 76: 177-190.
[3] NIGHTINGALE K K, THIPPAREDDI H, PHEBUS R K, et al. Validation of a traditional italian-style salami manufacturing process for control of Salmonella and Listeria monocytogenes[J]. Journal of Food Protection， 2006， 69(4): 794-800.
[4] JUNEJA V K， ALTUNTAŞ E G， AYHAN K， et al. Predictive model for the reduction of heat resistance of Listeria monocytogenesin ground beef by the combined effect of sodium chloride and apple polyphenols[J]. International Journal of Food Microbiology， 2013，164: 54-59.
[5] LEE Y L， JUNG B S， YOON H J， et al. Predictive model for the growth kinetics of Listeria monocytogenesin raw pork meat as a function of temperature[J]. Food Control， 2014， 44: 16-21.
[6] 李苗云， 张秋会， 赵改名， 等. 冷却猪肉中单增李斯特氏菌生长动力学模型的建立与评价[J]. 食品科学， 2009， 30(21): 234-236.
[7] de BLACKBURN C W， CURTIS L M， HUMPHESON L， et al. Development of thermal inactivation models for Salmonella enteritidisand Escherichia coliO157:H7 with temperature， pH and NaCl as controlling factors[J]. International Journal of Food Microbiology，1997， 38: 31-44.
[8] MCKELLAR R C， PERÉZ-RODRÍGUEZ F， HARRIS L J， et al. Evaluation of different approaches for modeling Escherichia coliO157:H7 survival on field lettuce[J]. International Journal of Food Microbiology， 2014， 184: 74-85.
[9] CHARIMBA G， HUGO C J， HUGO A. The growth， survival and thermal inactivation of Escherichia coliO157:H7 in a traditional South African sausage[J]. Meat Science， 2010， 85: 89-95.
[10] LE MARC Y， VALÍK L， MEDVE ĎOVÁ A. Modelling the effect of the starter culture on the growth of Staphylococcus aureusin milk[J]. International Journal of Food Microbiology， 2009， 129: 306-311.
[11] SCHEERANS C， WICHA S G， MICHAEL J， et al. Concentrationesponse studies and modelling of the pharmacodynamics of linezolid: Staphylococcus aureus versus Enterococcus faecium[J]. International Journal of Antimicrobial Agents， 2014， 4727: 1-7.
[12] PÉREZ-RODRÍGUEZ F， POSADA-IZQUIERDO G D， VALERO A， et al. Modelling survival kinetics of Staphylococcus aureusand Escherichia coliO157:H7 on stainless steel surfaces soiled with different substrates under static conditions of temperature and relative humidity[J]. Food Microbiology， 2013， 33: 197-204.
[13] 黄和， 李文杰， 雷晓凌， 等. 模拟蟹肉中金黄色葡萄球菌生长预测模型的研究[J]. 食品科技， 2010， 35(10): 54-57.
[14] BUENO E， GARCÍA P， MARTÍNEZ B， et al. Phage inactivation of Staphylococcus aureusin fresh and hard-type cheeses[J]. International Journal of Food Microbiology， 2012， 158: 23-27.
[15] 胡洁云， 欧杰， 李柏林. 预报微生物学在食品安全评估中的作用[J].微生物学通报， 2009， 36(9): 1397-1403.
[16] 李柏林， 郭剑飞， 欧杰. 预测微生物学数学建模的方法构建[J]. 食品科学， 2004， 25(11): 52-57.
[17] WHITING R C， BUCHANAN R L. Development of a quantitative risk assessment model for Salmonella enteritidisin pasteurized liquid eggs[J]. International Journal of Food Microbiology， 1997， 36(2): 111-125.
[18] 刘超群， 王宏勋， 侯温甫. 低温肉制品微生物控制与预测模型应用研究进展[J]. 食品科学， 2009， 30(21): 481-484.
[19] 董庆利， 屠康， 李保国， 等. 平方根模型在亚硝酸盐抑菌预测中的探讨研究[J]. 食品工业科技， 2009， 30(7): 161-164.
[20] 全国文献工作标准化技术委员会. GB/T 4789.10—2008 食品卫生微生物学检验 金黄色葡萄球菌检验[S]. 北京: 中国标准出版社， 2008.
[21] RESNIK S L， CHIRIFE J. Proposed theoretical a wvalues at various temperatures for selected solutions to be used as reference sources in the range of microbial growth[J]. Journal of Food Protection， 1988， 51: 419-423.
[22] BARANYI J， ROBERTS T A. A dynamic approach to predicting bacterial growth in food[J]. International Journal of Food Microbiology， 1994， 23: 277-294.
[23] ZWIETERING M H， ROMBOUTS F M， VAN T RIET K. Comparison of defi nitions of the lag phase and the exponential phase in bacterial growth[J]. Journal Applied of Bacteriology， 1996， 81(5): 501-508.
[24] SUTHERLAND J P， BAYLISS A J， BRAXTON D S， et al. Predictive modelling of Escherichia coliO157:H7: inclusion of carbon dioxide as a fourth factor in a pre-existing model[J]. International Journal of Food Microbiology， 1997， 37: 113-120.
[25] ROSS T. Indices for performance evaluation of predictive models in food microbiology[J]. Applied Bacteriology， 1996， 81(5): 501-508.
[26] STEWART C M， COLE M B， LEGAN J D， et al . Staphylococcus aureusgrowth boundaries: moving towards mechanistic predictive models based on solute-specifi c effects[J]. Applied and Environmental Microbiology， 2002， 68: 1864-1871.
[27] JEONG Dowon， HAN Seulhwa， LEE Jonghoon. Safety and technological characterization of Staphylococcus equorumisolates from jeotgal， a Korean high-salt-fermented seafood， for starter development[J]. International Journal of Food Microbiology， 2014，188: 108-115.
[28] XIONG R， XIE G， EDMONDSON A S， et al. Comparison of the Baranyi model with the modified Gompertz equation for modelling thermal inactivation of Listeria monocytogenesScott A[J]. Food Microbiology， 1999， 16(3): 269-279.
[29] 王虎虎， 董洋， 徐幸莲， 等. 酸化亚氯酸钠对鸡肉致病菌的致死模型研究[J]. 中国食品学报， 2013， 13(9): 33-38.
Modeling Staphylococcus aureusGrowth as a Function of Different Conditions in Nutrient Broth
LI Jinchun， ZHOU Tong， LI Jiapeng*， CHEN Xi， YANG Junna， XU Suigen， CHEN Wenhua
(Beijing Key Laboratory of Meat Processing Technology， China Meat Research Center， Beijing 100068， China)
Abstract：Effects of temperature， pH， and water activity (a w) on the growth of Staphylococcus aureusin nutrient broth medium were studied， respectively， and the first-order kinetics models of bacterial count (CFU) and the second-order kinetics models of maximum specifi c growth rate (μ max) and lag time were built subsequently. Results showed that increasing temperature， pH and a wcould increase the μ maxbut decrease the value of lag time. Colony-forming units (CFU) of S. aureus were modeled as a function of T， pH and a w， which revealed a good relationship as evaluated by the Baranyi model. The single-variable second-order models were evaluated by Bĕlehrádek square-root-type model with correlation coefficients more than 0.85. The multi-variable second-order models， namely polynomial logistic regression equations， were fi tted using a stepwise method with correlation coefficient more than 0.85. Then， the goodness of fit of the established models was evaluated by accuracy factor (A f)， bias factor (B f) and root mean square error (RMSE). It was found that their applicability，reliability and goodness of fi t were within acceptable ranges. The fi rst-order and second-order models provide a useful and accurate approach to predicting the growth of S. aureus within certain limits.
Key words： Staphylococcus aureus； nutrient broth medium； predictive microbiology； growth model
中图分类号：TS251.1
文献标志码：A
文章编号：1001-8123（2015）03-0005-06
doi：10.7506/rlyj1001-8123-201503002
收稿日期：2014-11-09
基金项目：国家高技术研究发展计划（863计划）项目（2011AA100805）
作者简介：李金春（1987—），男，助理工程师，硕士，研究方向为食品生物技术。E-mail：lijinchun1987@163.com
*通信作者：李家鹏（1979—），男，高级工程师，硕士，研究方向为食品生物技术。E-mail：ljp7915@yahoo.com.cn